10316. Ковшовая
бригада
На ферме вспыхнул пожар, и коровы
спешат его потушить! Ферма описывается таблицей 10 * 10 символов следующим
образом:
..........
..........
..........
..B.......
..........
.....R....
..........
..........
.....L....
..........
Символ B представляет сарай,
который только что загорелся. Символ L обозначает озеро, а R обозначает
местонахождение большого камня.
Коровы хотят сформировать “бригаду ведер”, расположившись вдоль тропы между озером и коровником,
чтобы они могли передавать по тропинке ведра с водой для тушения пожара. Ковш
может перемещаться между коровами, если они непосредственно примыкают по
вертикали или по горизонтали. То же самое и с коровой, стоящей рядом с озером:
корова может вытащить ведро воды из озера, только если она находится
непосредственно рядом с озером. Точно так же корова может вылить ведро с водой
в стойло, только если она находится непосредственно рядом со стойлом.
Определите минимальное количество ‘.’ квадратов, которые следует занять коровам чтобы сформировать успешную
бригаду ведер.
Корова не может быть размещена на
квадрате, содержащем большой камень, а сарай и озеро гарантированно не
примыкают друг к другу.
Вход. Содержит 10 строк,
каждая из которых содержит 10 символов,
описывающих план фермы.
Выход. Выведите одно целое число – минимальное количество коров, необходимое для формирования жизнеспособной бригады ведер.
Пример. Ниже приведено одно из возможных решений, которое включает оптимальное количество
коров (7):
..........
..........
..........
..B.......
..C.......
..CC.R....
...CCC....
.....C....
.....L....
..........
|
Пример
входа |
Пример
выхода |
|
.......... .......... .......... ..B....... .......... .....R.... .......... .......... .....L.... .......... |
7 |
РЕШЕНИЕ
математика
Анализ алгоритма
Введем систему координат.
Например, пусть верхний левый угол имеет координаты (0, 0). Найдем координаты сарая
(bx, by), озера (lx,
ly) и камня (rx, ry).
Далее
находим манхетенские расстояния:
·
dBL = BarnLake – между сараем и озером;
·
dBR = BarnRock – между сараем и камнем;
·
dLR = LakeRock – между озером и камнем;
Манхетенское расстояние
между объектами A(x1, y1) и B(x2, y2) вычисляетя по
формуле: dAB = | x2 – x1
| + | y2 – y1 |.
Если не
учитывать камень, то количество коров в бригаде должно равняться манхетенскому расстоянию
между сараем и озером минус один.
Требуемое число
коров увеличится на 2, только если сарай и озеро находятся на одной горизонтальной или
вертикальной прямой, а камень лежит на пути между ними. Последнее условие истинно,
если dBL = dBR + dLR.
Сарай и озеро лежат на горизонтальной
прямой, если by = ly.
Сарай и озеро лежат на вертикальной
прямой, если bx = lx.
Пример
Для заданного
примера объекты имеют следующие координаты: сарай (3, 2), озеро
(8, 5) и камень (5, 5). Манхетенское расстояние между сараем и
озером равно | 8 – 3 | + | 5 – 2 | = 8. Требуемое
число коров равно 8 – 1 = 7.
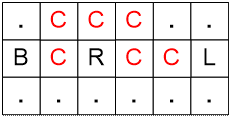
Рассмотрим
следующий пример, когда камень лежит между сараем и озером. Расстояние между сараем
и озером равно 5. Число коров без учета камня требуется 4. Однако для обхода
камня потребуется 4 + 2 = 6 коров.
Реализация алгоритма
Читаем входные данные. Размер входного поля 10 * 10.
for (i = 0; i < 10; i++)
cin >> s[i];
Находим координаты сарая (bx, by), озера (lx,
ly) и камня (rx, ry).
for (i = 0; i < 10; i++)
for (j = 0; j < 10; j++)
{
if
(s[i][j] == 'R') { rx = i; ry = j; }
if
(s[i][j] == 'B') { bx = i; by = j; }
if
(s[i][j] == 'L') { lx = i; ly = j; }
}
Находим расстояния:
·
BarnLake – между сараем и озером;
·
BarnRock – между сараем и камнем;
·
LakeRock – между озером и камнем;
BarnLake
= abs(bx - lx) + abs(by - ly);
BarnRock
= abs(bx - rx) + abs(by - ry);
LakeRock
= abs(lx - rx) + abs(ly - ry);
Находим
количество res коров, необходимое для формирования бригады между сараем
и озером. Оно на единицу меньше манхетенского расстояния
между (bx, by) и (lx, ly).
res
= BarnLake - 1;
Если
сарай и озеро находятся на одной горизонтали или вертикали, а камень лежит на
пути между ними, то количество коров для построения пути следует увеличить на
2.
if ((BarnLake == BarnRock +
LakeRock) && (bx == lx || by == ly))
res += 2;
Выводим
ответ.
cout
<< res << endl;